↗ arXiv ↗ Hugging Face ↗ Papers with Code
TL;DR#
대규모 언어 모델(LLM) 훈련 비용을 줄이기 위해 저정밀도 훈련이 널리 사용되고 있습니다. 기존 연구는 주로 정수 양자화에 초점을 맞춰 부동 소수점 양자화의 특성을 고려하지 못했고, 실제 환경에서의 부동 소수점 양자화 훈련에 대한 연구는 미흡했습니다. 특히, 지수 비트와 맨티사 비트의 최적 비율, 스케일링 인자의 계산 정밀도 등이 모델 성능에 미치는 영향에 대한 이해가 부족했습니다.
본 논문에서는 LLM의 부동 소수점 양자화 훈련 성능에 대한 새로운 scaling law를 제시합니다. 데이터 크기, 모델 크기, 지수 비트, 맨티사 비트, 스케일링 인자의 블록 크기 등 다양한 요소들을 고려하여 실험을 통해 검증했습니다. 최적의 지수-맨티사 비트 비율, 임계 데이터 크기, 비용 대비 성능이 가장 좋은 정밀도 등을 제시하고, 향후 하드웨어 설계 및 LLM 훈련에 대한 유용한 지침을 제공합니다.
Key Takeaways#
Why does it matter?#
본 논문은 낮은 정밀도 부동 소수점 양자화 훈련에 대한 새로운 scaling law를 제시하여, LLM 훈련의 효율성과 비용을 크게 개선할 수 있는 잠재력을 가지고 있습니다. 하드웨어 제조업체를 위한 최적의 지수-맨티사 비트 비율 제시, 임계 데이터 크기 발견, 비용 대비 성능이 가장 좋은 정밀도 제안 등의 결과는 향후 연구 방향을 제시하고, 저전력 및 저비용 LLM 개발에 중요한 영향을 미칠 수 있습니다. 본 논문은 실제 응용과 이론적 통찰 간의 격차를 해소하고, 보다 정확하고 예측 가능한 scaling law를 제공하여, 향후 연구에 중요한 기여를 할 수 있습니다.
Visual Insights#

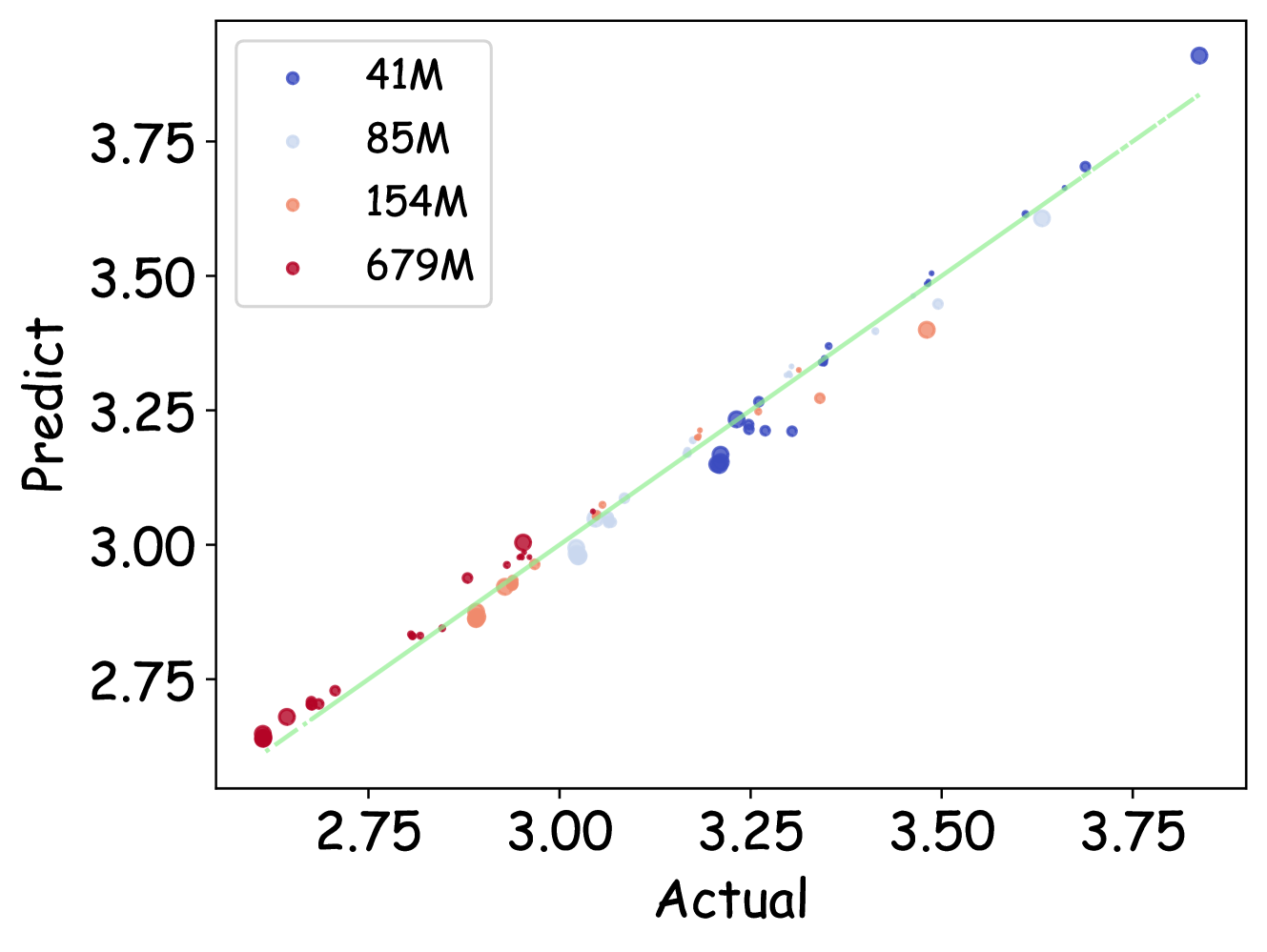
🔼 그림 1은 Kumar et al. (2024)의 연구에서 제시된 방정식 (7)을 기반으로 하는 스케일링 법칙의 적합 결과를 보여줍니다. 특히, E1M1 경우 큰 편차가 있음을 보여줍니다. 그림의 왼쪽, 가운데, 오른쪽의 세 개의 하위 그림은 각각 데이터 크기(D), 지수 비트(E), 가수 비트(M)에 대략적으로 비례하는 데이터 점의 크기를 나타냅니다. 이는 저차원의 부동소수점 양자화 훈련에서 각 매개변수가 성능에 미치는 영향을 시각적으로 보여줍니다.
read the caption
Figure 1: The fitting results of the scaling law in Eq. (7) deriving from Kumar et al. (2024), which have large bias in E1M1 case. In the three sub-figures on the left, middle and right, the sizes of the data points are approximately proportional to D𝐷Ditalic_D, E𝐸Eitalic_E, and M𝑀Mitalic_M respectively.
| Hyper-parameters | 41M | 85M | 154M | 679M | 1.2B | |
|---|---|---|---|---|---|---|
| Layers | 12 | 12 | 12 | 24 | 24 | |
| Hidden Size | 512 | 768 | 1024 | 1536 | 2048 | |
| FFN Hidden Size | 1536 | 2048 | 2816 | 4096 | 5632 | |
| Attention Heads | 8 | 12 | 16 | 24 | 32 | |
| Attention Head size | 64 | 64 | 64 | 64 | 64 | |
| Optimizer | AdamW | AdamW | AdamW | AdamW | AdamW | |
| Adam (β1,β2) | (0.9, 0.95) | (0.9, 0.95) | (0.9, 0.95) | (0.9, 0.95) | (0.9, 0.95) | |
| Adam ϵ | 1×10−8 | 1×10−8 | 1×10−8 | 1×10−8 | 1×10−8 | |
| Weight Decay | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | |
| Clip Grad Norm | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | |
| Max LR | 3.0×10−4 | 3.0×10−4 | 3.0×10−4 | 3.0×10−4 | 3.0×10−4 | |
| Min LR | 0 | 0 | 0 | 0 | 0 | |
| LR Decay | Cosine | Cosine | Cosine | Cosine | Cosine | |
| Seqence Length | 2048 | 2048 | 2048 | 2048 | 2048 | |
| Batch Size (# Tokens) | 2M | 2M | 2M | 2M | 2M | |
| Warmup Steps | 500 | 500 | 500 | 500 | 500 |
🔼 이 표는 논문의 실험에 사용된 다양한 크기의 LLaMA 모델에 대한 초매개변수를 보여줍니다. 각 모델 크기(41M, 85M, 154M, 679M, 1.2B 매개변수)에 대해 레이어 수, 은닉 크기, FFN 은닉 크기, 어텐션 헤드 수, 어텐션 헤드 크기, 최적화기, 옵티마이저의 하이퍼파라미터(AdamW, Adam의 β1과 β2, Adam ε, 가중치 감소, 경사 클리핑 놈, 최대 학습률, 최소 학습률, 학습률 감소, 시퀀스 길이, 배치 크기, 웜업 단계 등), 등의 세부 정보가 포함되어 있습니다. 이러한 초매개변수는 논문에서 수행된 다양한 저정밀도 실험을 위한 기반을 마련합니다.
read the caption
Table 1: Model hyper-parameters for each size.
In-depth insights#
FP Quant. Scaling Laws#
본 논문에서 제시된 ‘FP Quant. Scaling Laws’는 부동소수점(FP) 양자화 훈련의 성능에 영향을 미치는 주요 요소들 간의 관계를 수학적으로 표현한 공식입니다. 이는 단순히 정확도 손실을 예측하는 것을 넘어, 최적의 비트 수, 지수 비트 수, 가수 비트 수, 그리고 스케일링 팩터의 계산 방식 등을 결정하는 데 중요한 통찰력을 제공합니다. 특히, 지수 비트가 가수 비트보다 모델 성능에 더 큰 영향을 미치며, 최적의 비트 할당 비율을 제시한다는 점은 하드웨어 설계에 직접적인 시사점을 줍니다. 또한, 훈련 데이터의 양이 일정 수준을 넘어서면 오히려 성능이 저하될 수 있으며, 이러한 임계점을 예측하는 방법도 제시되어 있습니다. 계산 성능과 비용 효율성을 고려한 최적의 양자화 정밀도는 4~8비트 사이에 존재한다는 결론은 실제 응용에 중요한 지침이 됩니다. 결론적으로, 본 논문은 실제적인 FP 양자화 훈련에 대한 보다 정교하고 정확한 스케일링 법칙을 제시함으로써, LLM 개발 및 최적화에 대한 새로운 가능성을 열어줍니다.
LLM Precision Limits#
LLM의 정밀도 한계에 대한 심층적인 논의는 모델 성능과 계산 비용 간의 균형을 이루는 데 매우 중요합니다. 낮은 정밀도를 사용하면 메모리 사용량과 연산량을 줄일 수 있지만, 모델 성능 저하로 이어질 수 있습니다. 따라서, 최적의 정밀도 수준을 결정하는 것은 LLM 개발의 핵심적인 과제입니다. 이는 단순히 비트 수를 줄이는 것 이상으로, 지수부와 가수부 비트 할당, 계산 과정의 양자화 대상, 그리고 스케일링 팩터의 블록 크기 등 다양한 요소들을 고려해야 함을 시사합니다. 본 연구는 부동 소수점 양자화 훈련에 대한 스케일링 법칙을 제시하여, 이러한 요소들이 LLM 성능에 미치는 영향을 정량적으로 분석합니다. 최적의 비용-성능을 달성하기 위한 정밀도 수준과 데이터 크기, 모델 크기의 상호작용을 밝히는 것은 향후 연구의 중요한 방향입니다.
Optimal Bit Allocation#
본 논문에서 다룬 최적 비트 할당(Optimal Bit Allocation)은 부동 소수점 양자화 훈련에서 모델 성능을 극대화하기 위한 지수 비트와 가수 비트의 최적 배분을 결정하는 문제입니다. 정확도와 효율성 사이의 균형을 맞추는 것이 중요하며, 이는 계산 능력과 훈련 데이터 크기에 따라 달라집니다. 논문에서는 최적의 지수-가수 비트 비율을 제시하고, 이를 통해 비용 대비 성능이 가장 좋은 정밀도를 찾아내는 데 도움이 되는 통찰력을 제공합니다. 훈련 데이터 크기가 증가함에 따라 최적의 정밀도도 증가하지만, 어느 시점을 넘어서면 성능 저하가 발생하는 임계 데이터 크기의 존재를 밝혔습니다. 이는 제한된 계산 자원 하에서 최적의 성능을 얻기 위한 중요한 고려 사항이며, 할당된 비트 수 대비 최대 성능을 유지하기 위한 전략을 세우는 데 도움이 됩니다.
Quant. Target Effects#
본 논문에서 다루는 양자화 대상 효과는 LLM(대규모 언어 모델)의 성능에 미치는 다양한 입력값의 양자화 영향을 분석한 부분입니다. 연구에서는 변환기 아키텍처 내 GEMM(일반 행렬 곱셈) 계산에 대한 입력값 6가지(X, W, dY1, Wbwd, dY2, Xbwd)를 각각 양자화했을 때의 영향을 실험적으로 조사했습니다. 그 결과, 특정 입력값(P1, P3, P5)의 양자화는 손실 증가로 이어져 모델 성능 저하를 초래하지만, 다른 입력값(P4, P6)의 양자화는 오히려 성능 개선을 가져오는 것을 확인했습니다. 특히 P5(역전파 과정의 입력 임베딩)의 양자화는 성능 저하가 매우 컸습니다. 따라서, 성능과 효율성 간의 균형을 고려하여 P2, P4, P6만을 양자화하는 것이 최적의 전략임을 제시합니다. 이러한 분석을 통해 양자화 전략의 세밀한 조정이 LLM의 성능 향상에 중요한 역할을 한다는 점을 보여줍니다. 향후 연구는 제시된 최적 전략을 바탕으로 저정밀도 LLM 훈련을 위한 심층적인 연구를 수행할 수 있습니다.
Future Research#
본 논문은 부동 소수점 양자화 훈련에 대한 확장 법칙을 제시하고 다양한 비트 너비 설정에서의 성능을 예측하는 데 성공했습니다. 하지만, 여러 가지 제한점이 있습니다. 우선, 현재 실험은 주로 Transformer 아키텍처에 기반한 LLM에 집중되어 있어 다른 아키텍처에도 적용 가능한지 추가 연구가 필요합니다. 또한, 다양한 양자화 기법의 영향을 좀 더 심층적으로 분석하여 다양한 양자화 방법론의 확장 법칙을 개발해야 합니다. 더불어, 더 큰 모델 및 더 많은 데이터에 대한 확장 법칙 검증 및 실제 하드웨어 환경에서의 성능 평가를 통해 실제 적용 가능성을 높여야 합니다. 마지막으로, 본 논문에서 제시된 최적의 비트 할당 전략이 다양한 모델 크기 및 데이터 크기에 대해 얼마나 견고한지를 확인하는 추가 연구가 필요하며, 비용 효율적인 양자화 전략 개발을 위한 연구도 필요합니다. 미래 연구는 이러한 제한점을 해결하고 본 논문의 결과를 보다 폭넓게 적용하는 데 집중해야 할 것입니다.
More visual insights#
More on figures

🔼 그림 2(a)는 Chinchilla scaling law를 사용하여 예측한 손실 값과 실제 훈련 손실 값을 비교한 그래프입니다. Chinchilla scaling law는 모델 크기(N)와 데이터 크기(D)가 훈련 손실(L)에 미치는 영향을 설명하는 기존의 scaling law 중 하나입니다. 이 그래프는 Chinchilla scaling law가 다양한 모델 크기와 데이터 크기에 대해 실제 훈련 손실을 잘 예측함을 보여줍니다. 데이터 점의 크기는 데이터 크기(D)에 비례합니다.
read the caption
(a) Chinchilla basic scaling law.

🔼 그림은 OpenAI 스케일링 법칙을 사용하여 예측된 손실과 실제 훈련 손실 간의 적합성을 보여줍니다. Chinchilla 스케일링 법칙과 비교하여 OpenAI 스케일링 법칙의 적합성이 다소 떨어지는 것을 알 수 있습니다. 데이터 포인트의 크기는 데이터 크기(D)에 비례합니다.
read the caption
(b) OpenAI basic scaling law.

🔼 그림 2는 기존의 확장 법칙(Chinchilla 및 OpenAI)의 적합도를 보여줍니다. x축은 실제 손실, y축은 예측 손실을 나타냅니다. 데이터 포인트의 크기는 데이터 크기(D)에 비례합니다. 각 점은 특정 모델 크기(N)와 데이터 크기(D) 조합에서의 훈련 손실을 나타내며, 기존 확장 법칙이 얼마나 잘 실제 손실을 예측하는지 보여줍니다. Chinchilla 법칙이 OpenAI 법칙보다 실제 손실을 더 잘 예측하는 것을 알 수 있습니다.
read the caption
Figure 2: The fitting performance of classical scaling laws. The size of the data point is proportional to D𝐷Ditalic_D.

🔼 본 그림은 Transformer 아키텍처 내 GEMM(General Matrix Multiplication) 연산에 대한 입력 텐서의 양자화 대상을 보여줍니다. Transformer는 순전파, 입력 그래디언트 계산, 가중치 그래디언트 계산의 세 가지 주요 GEMM 연산을 포함합니다. 이러한 행렬 곱셈의 입력은 X, W, dY1, Wbwd, dY2, Xbwd의 여섯 가지 고유한 요소로 구성됩니다. 이러한 요소들을 P1~P6으로 나타내고, 그림에서는 각 요소가 어떤 연산에 입력되는지, 그리고 순전파/역전파 과정에서 어떤 연산에 사용되는지를 시각적으로 보여줍니다. 논문에서는 이 중 P2, P4, P6을 양자화 대상으로 선택하고, 이후 스케일링 법칙 탐구에 사용합니다.
read the caption
Figure 3: Quantization Targets. We select P2, P4, and P6 as our quantization targets for the following exploration of scaling laws.

🔼 그림 4는 Transformer 아키텍처 내 GEMM(General Matrix Multiplication) 연산에 대한 다양한 양자화 목표(quantization targets)의 결과를 보여줍니다. 각 목표는 Transformer의 순방향(forward) 및 역방향(backward) 패스에서의 6가지 다른 입력(X, W, dY1, Wbwd, dY2, Xbwd)을 나타냅니다. 이 그림은 각 양자화 목표를 개별적으로 또는 조합하여 양자화했을 때 손실(loss)의 변화를 비교 분석하여 어떤 입력의 양자화가 모델 성능에 가장 큰 영향을 미치는지 보여줍니다. 특히, 특정 입력의 양자화가 성능 저하를 크게 유발할 수 있음을 시각적으로 보여줍니다. 이는 모델 성능을 최적화하기 위해 어떤 입력을 양자화해야 하는지에 대한 중요한 통찰력을 제공합니다.
read the caption
Figure 4: Results of loss gaps with different quantization targets.

🔼 그림 5는 지수 관련 스케일링 법칙에서의 γ와 ι의 상관관계를 보여줍니다. γ와 ι는 N과 D의 함수로 볼 수 있으며, 데이터 포인트의 크기는 D에 비례합니다. 이 그림은 모델 크기(N)와 데이터 크기(D)가 다양할 때, 지수(E)에 대한 스케일링 법칙을 더 잘 이해하는 데 도움이 되는 시각적 자료입니다. γ와 ι는 각각 모델 크기와 데이터 크기와 어떤 상관관계를 가지는지, 그리고 그 상관관계가 어떻게 데이터 크기에 따라 변화하는지를 보여줍니다.
read the caption
Figure 5: The correlations between γ𝛾\gammaitalic_γ,ι𝜄\iotaitalic_ι in Eq. (12) and N𝑁Nitalic_N,D𝐷Ditalic_D. γ𝛾\gammaitalic_γ,ι𝜄\iotaitalic_ι could be viewed as functions of N𝑁Nitalic_N,D𝐷Ditalic_D. Data point size is proportional to D𝐷Ditalic_D.

🔼 그림 6은 제시된 지수 관련 스케일링 법칙의 적합도를 보여줍니다. 이 그림은 다양한 모델 크기(N), 데이터 크기(D), 지수(E) 설정에서의 실험 결과를 보여주며, 스케일링 법칙이 실제 손실 값을 얼마나 정확하게 예측하는지 보여줍니다. 데이터 포인트 크기는 데이터 크기(D)에 비례합니다. 이를 통해 지수 비트가 모델 성능에 미치는 영향과 스케일링 법칙의 정확성을 시각적으로 파악할 수 있습니다.
read the caption
Figure 6: The fitting results of our Exponent-related scaling law. Data point size is proportional to D𝐷Ditalic_D.

🔼 그림 7은 제시된 논문에서 제안된 Mantissa 관련 스케일링 법칙의 적합도를 보여줍니다. 그림은 다양한 모델 크기(N), 데이터 크기(D), Mantissa 비트(M)에 대한 실험 결과를 보여주며, 각 점의 크기는 데이터 크기(D)에 비례합니다. 이를 통해 Mantissa 비트 수가 모델 성능에 미치는 영향과 제안된 스케일링 법칙의 정확성을 시각적으로 확인할 수 있습니다. 그림은 제안된 스케일링 법칙이 실제 손실 값을 얼마나 정확하게 예측하는지 보여주는 산점도를 나타냅니다.
read the caption
Figure 7: The fitting results of our Mantissa-related scaling law. Data point size is proportional to D𝐷Ditalic_D.

🔼 그림 8은 지수와 가수 비트 수에 대한 스케일링 법칙의 적합 결과를 보여줍니다. 왼쪽, 가운데, 오른쪽 하위 그림의 데이터 점 크기는 각각 데이터 크기(D), 가수 비트 수(M), 지수 비트 수(E)에 비례합니다. 이 그림은 서로 다른 데이터 크기, 가수 비트 수, 지수 비트 수 조합에 대해 훈련된 다양한 모델의 손실을 시각적으로 보여줍니다. 이를 통해 지수 비트와 가수 비트가 모델 성능에 미치는 영향과 최적의 비트 할당을 파악하는 데 도움이 됩니다.
read the caption
Figure 8: The fitting results of the joint Exponent & Mantissa scaling law: Data point sizes in left, middle, and right sub-figures are proportional to D𝐷Ditalic_D, M𝑀Mitalic_M, and E𝐸Eitalic_E, respectively.

🔼 그림 9는 논문의 3.6절, 블록 크기 관련 스케일링 법칙에서 다루는 내용을 보여줍니다. 이 그림은 방정식 (19)에서 설명하는 κ와 ψ가 모델 크기(N)와 데이터 크기(D)에 따라 어떻게 변하는지를 보여주는 산점도입니다. 각 점의 크기는 데이터 크기(D)에 비례하여 표시됩니다. 즉, 데이터 크기가 클수록 점의 크기가 커집니다. 이 그림은 블록 크기에 따른 스케일링 법칙을 이해하는 데 중요한 시각적 자료로, κ와 ψ가 모델과 데이터 크기에 따라 어떻게 변화하는지, 그리고 그 관계가 어떤지를 보여줍니다. 특히, κ는 D와 양의 상관관계를, ψ는 D와 음의 상관관계를 가지는 것을 시각적으로 확인할 수 있습니다.
read the caption
Figure 9: The correlations between κ𝜅\kappaitalic_κ,ψ𝜓\psiitalic_ψ in Eq. (19) and N𝑁Nitalic_N,D𝐷Ditalic_D. κ𝜅\kappaitalic_κ,ψ𝜓\psiitalic_ψ could be viewed as functions of N𝑁Nitalic_N,D𝐷Ditalic_D. The data points are scaled proportionally to the value of D𝐷Ditalic_D.
🔼 그림 10은 제안된 스케일링 법칙이 다양한 블록 크기에 대해 검증 손실을 정확하게 예측함을 보여줍니다. 왼쪽과 오른쪽 하위 그림에서 데이터 점의 크기는 각각 데이터 크기(D)와 블록 크기(B)에 정비례합니다. 이는 제안된 스케일링 법칙이 다양한 블록 크기에 대해서도 정확하게 검증 손실을 예측할 수 있음을 시각적으로 보여줍니다. 데이터 크기와 블록 크기가 스케일링 법칙의 정확도에 미치는 영향을 명확하게 보여줍니다.
read the caption
Figure 10: Our scaling law precisely forecasts validation loss for diverse block sizes. Data point sizes are directly proportional to D𝐷Ditalic_D and B𝐵Bitalic_B in the respective left and right sub-figures.

🔼 그림 11은 채널 방식 스케일링 법칙의 적합 결과를 보여줍니다. 데이터 포인트의 크기는 데이터 크기(D)에 비례합니다. 이 그림은 모델 크기(N)과 데이터 크기(D)가 주어졌을 때, 채널 단위로 스케일링 인자의 블록 크기(B)를 변경했을 때의 손실(Loss) 변화를 보여줍니다. 이를 통해 채널 방식 스케일링 법칙이 실제 손실 값을 얼마나 잘 예측하는지 확인할 수 있습니다. 각 점의 크기는 데이터 크기(D)에 비례하여, 데이터 크기가 클수록 점의 크기가 커집니다.
read the caption
Figure 11: The fitting results of the channel-wise scaling law. The size of the data point is proportional to D𝐷Ditalic_D.

🔼 그림 12는 블록 크기(B)의 로그 값과 N/D(모델 크기/데이터 크기)의 관계를 보여줍니다. 각 점의 크기는 데이터 크기(D)에 비례합니다. 이 그림은 서로 다른 모델 크기와 데이터 크기를 가진 여러 실험 결과를 보여주며, 블록 크기가 모델 성능에 미치는 영향을 시각적으로 보여줍니다. 특히, N/D 값이 클수록 블록 크기의 로그 값이 작아지는 경향이 있습니다. 이는 데이터 크기가 클 때 더 작은 블록 크기를 사용하는 것이 효율적일 수 있음을 시사합니다.
read the caption
Figure 12: The correlations between log2Bsubscript2𝐵\log_{2}Broman_log start_POSTSUBSCRIPT 2 end_POSTSUBSCRIPT italic_B and ND𝑁𝐷\frac{N}{D}divide start_ARG italic_N end_ARG start_ARG italic_D end_ARG. The size of the data point is proportional to D𝐷Ditalic_D.

🔼 그림 13은 텐서 단위 스케일링 법칙의 적합 결과를 보여줍니다. 데이터 포인트의 크기는 데이터 크기(D)에 비례합니다. 이 그림은 저정밀도 부동 소수점 양자화 훈련에서 텐서 크기(B)의 영향을 시각적으로 보여줍니다. x축은 실제 손실 값을, y축은 예측 손실 값을 나타냅니다. 데이터 포인트의 크기가 클수록 데이터 크기가 크다는 것을 의미합니다. 이를 통해 큰 데이터셋에서 텐서 크기가 모델 성능에 미치는 영향을 분석할 수 있습니다.
read the caption
Figure 13: The fitting results of the tensor-wise scaling law. The size of the data point is proportional to D𝐷Ditalic_D.

🔼 그림 14는 제시된 논문의 부동 소수점 양자화 훈련에 대한 스케일링 법칙의 적합 결과를 보여줍니다. 데이터 포인트의 크기는 데이터셋 크기(D)에 비례합니다. 별표로 표시된 12억 매개변수 모델들은 검증에 사용된 모델들을 나타냅니다. 이 그림은 스케일링 법칙이 다양한 모델 크기와 데이터셋 크기에 걸쳐 실제 손실을 얼마나 잘 예측하는지를 보여줍니다. 특히, 별표로 표시된 검증 데이터에 대한 예측 성능은 스케일링 법칙의 일반화 성능을 평가하는 데 중요한 지표입니다.
read the caption
Figure 14: The fitting results of our scaling law for floating-point quantization training. Data point size is proportional to D𝐷Ditalic_D. The star points (1.2B models) are our validation.

🔼 그림 15는 다양한 비트 너비에 대한 최적의 부동 소수점 레이아웃을 보여줍니다. x축은 mantissa 비트 수, y축은 exponent 비트 수를 나타내며, 각 점은 특정 비트 너비에 대한 최적의 exponent/mantissa 비율을 나타냅니다. 이 그림은 논문에서 제시된 최적화된 부동 소수점 양자화 방법을 시각적으로 보여주는 역할을 합니다. FP4, FP8, FP16과 같은 다양한 정밀도에서 최적의 exponent/mantissa 비율을 확인할 수 있습니다. 이를 통해, 주어진 비트 너비 내에서 모델 성능을 극대화할 수 있는 최적의 부동 소수점 표현 방식을 선택하는 데 도움이 됩니다.
read the caption
Figure 15: The optimal float layouts of different bit widths.

🔼 그림 16은 서로 다른 부동 소수점 양자화 설정에서 데이터 크기에 따른 손실 변화를 보여줍니다. 각 그래프는 고정된 지수 비트(E)와 mantissa 비트(M)를 가지는 모델에 대해, 데이터 크기(D)가 증가함에 따라 손실이 어떻게 변하는지 보여줍니다. 여러 데이터 크기와 양자화 설정에서 모델 성능에 미치는 영향을 시각적으로 비교하여, 최적의 양자화 전략을 선택하는 데 도움이 됩니다. 세 개의 그래프 모두 데이터 크기가 증가하면서 손실이 감소하다가 특정 지점을 넘어서면 다시 증가하는 것을 보여주는 데, 이는 과도한 데이터로 인한 성능 저하를 시사합니다. 이는 특정 양자화 설정에서 최적의 데이터 크기가 존재함을 나타냅니다.
read the caption
Figure 16: Variation of loss with data size under different floating-point quantization settings.

🔼 그림 17은 계산 비용이 제한된 상황(블록 크기 B는 128로 고정)에서 실험 데이터 피팅 결과를 바탕으로 다양한 데이터 크기(D)에 대한 최적의 정밀도(P) 값을 보여줍니다. 0.1T에서 100T까지의 넓은 데이터 크기 범위에서 최적의 정밀도 값은 일관되게 4
8비트 범위 내에 있음을 보여줍니다. 즉, 데이터 크기가 증가함에 따라 더 높은 정밀도가 필요하지 않으며, 계산 비용을 고려했을 때 48비트의 정밀도가 비용 대비 성능 면에서 효율적임을 시사합니다.read the caption
Figure 17: Under the constraint of computing the budget with block size (B𝐵Bitalic_B) set to 128, and based on the results of our experimental data fitting, the optimal precision (P𝑃Pitalic_P) values for different data sizes (D𝐷Ditalic_D) can be deduced. As depicted, across a substantially broad range of data sizes from 0.1T to 100T, the optimal precision value consistently falls within the range of 4 to 8 bits.

🔼 그림 18은 총 연산 비용에 따른 최적의 비용-성능 측면의 정밀도를 보여줍니다. 블록 크기(B)가 128이고 k가 6/16일 때 정밀도(P)와 연산 비용(C)의 관계를 보여줍니다. 이 그림은 제한된 연산 비용 내에서 최적의 정밀도를 선택하는 데 도움이 되는 정보를 제공합니다. 즉, 연산 비용이 증가함에 따라 최적의 정밀도도 증가하지만, 특정 지점을 넘어서면 정밀도가 감소함을 보여줍니다. 이는 제한된 자원 내에서 최적의 성능을 얻기 위해 정밀도와 연산 비용 간의 균형을 맞춰야 함을 시사합니다.
read the caption
Figure 18: The optimal cost-performance ratio precision as a function of the total compute budget, illustrating the relationship between precision (P𝑃Pitalic_P) and computational budget (C𝐶Citalic_C) when the block size (B𝐵Bitalic_B) is set to 128 and k=6/16𝑘616k=6/16italic_k = 6 / 16.
More on tables
| Constant | Value |
|---|---|
| n | 69.2343 |
| α | 0.2368 |
| d | 68973.0621 |
| β | 0.5162 |
| ϵ | 1.9061 |
| γ | 11334.5197 |
| δ | 3.1926 |
| ν | 2.9543 |
🔼 본 논문에서 제안하는 부동 소수점 양자화 훈련을 위한 통합 스케일링 법칙에 사용된 적합된 초매개변수와 해당 값을 보여주는 표입니다. 표에는 통합 스케일링 법칙의 정확도에 영향을 미치는 여러 요소 (데이터 크기, 모델 크기, 지수 비트, 가수 비트, 스케일링 계수의 블록 크기)를 고려하여 도출한 초매개변수 (a, β, γ, δ, ν)의 값이 포함되어 있습니다. 이러한 초매개변수는 다양한 모델 크기, 데이터 크기 및 양자화 설정에서 실험을 통해 얻어진 결과를 기반으로 합니다. 이 표는 본 논문의 스케일링 법칙을 이해하고 해석하는 데 중요한 역할을 합니다.
read the caption
Table 2: Fitted hyper-parameters and their values in our proposed unified scaling law for floating-point quantization training.
| N | D | E | M | B | Fitting support | |
| 0 | 40894464 | 10485760000 | 0 | 7 | channel | ✓ |
| 1 | 40894464 | 10485760000 | 1 | 1 | 32 | ✓ |
| 2 | 40894464 | 10485760000 | 1 | 1 | 64 | ✓ |
| 3 | 40894464 | 10485760000 | 1 | 1 | 128 | ✓ |
| 4 | 40894464 | 10485760000 | 1 | 1 | 256 | ✓ |
| 5 | 40894464 | 10485760000 | 1 | 1 | 512 | ✓ |
| 6 | 40894464 | 10485760000 | 1 | 1 | channel | ✓ |
| 7 | 40894464 | 10485760000 | 1 | 1 | tensor | ✓ |
| 8 | 40894464 | 10485760000 | 1 | 2 | channel | ✓ |
| 9 | 40894464 | 10485760000 | 1 | 3 | channel | ✓ |
| 10 | 40894464 | 10485760000 | 1 | 4 | channel | ✓ |
| 11 | 40894464 | 10485760000 | 1 | 5 | channel | ✓ |
| 12 | 40894464 | 10485760000 | 1 | 6 | channel | ✓ |
| 13 | 40894464 | 10485760000 | 2 | 1 | channel | ✓ |
| 14 | 40894464 | 10485760000 | 2 | 3 | channel | ✓ |
| 15 | 40894464 | 10485760000 | 3 | 1 | channel | ✓ |
| 16 | 40894464 | 10485760000 | 3 | 2 | channel | ✓ |
| 17 | 40894464 | 10485760000 | 4 | 1 | channel | ✓ |
| 18 | 40894464 | 10485760000 | 4 | 3 | channel | ✓ |
| 19 | 40894464 | 10485760000 | 4 | 5 | channel | ✓ |
| 20 | 40894464 | 10485760000 | 5 | 1 | channel | ✓ |
| 21 | 40894464 | 10485760000 | 5 | 2 | channel | ✓ |
| 22 | 40894464 | 10485760000 | 6 | 1 | channel | ✓ |
| 23 | 40894464 | 20971520000 | 0 | 7 | channel | ✓ |
| 24 | 40894464 | 20971520000 | 1 | 1 | 32 | ✓ |
| 25 | 40894464 | 20971520000 | 1 | 1 | 64 | ✓ |
| 26 | 40894464 | 20971520000 | 1 | 1 | 128 | ✓ |
| 27 | 40894464 | 20971520000 | 1 | 1 | 256 | ✓ |
| 28 | 40894464 | 20971520000 | 1 | 1 | 512 | ✓ |
| 29 | 40894464 | 20971520000 | 1 | 1 | channel | ✓ |
| 30 | 40894464 | 20971520000 | 1 | 1 | tensor | ✓ |
| 31 | 40894464 | 20971520000 | 1 | 2 | channel | ✓ |
| 32 | 40894464 | 20971520000 | 1 | 3 | channel | ✓ |
| 33 | 40894464 | 20971520000 | 1 | 4 | channel | ✓ |
| 34 | 40894464 | 20971520000 | 1 | 5 | channel | ✓ |
| 35 | 40894464 | 20971520000 | 1 | 6 | channel | ✓ |
| 36 | 40894464 | 20971520000 | 2 | 1 | channel | ✓ |
| 37 | 40894464 | 20971520000 | 2 | 3 | channel | ✓ |
| 38 | 40894464 | 20971520000 | 3 | 1 | channel | ✓ |
| 39 | 40894464 | 20971520000 | 3 | 2 | channel | ✓ |
| 40 | 40894464 | 20971520000 | 4 | 1 | channel | ✓ |
| 41 | 40894464 | 20971520000 | 4 | 3 | channel | ✓ |
| 42 | 40894464 | 20971520000 | 4 | 5 | channel | ✓ |
| 43 | 40894464 | 20971520000 | 5 | 1 | channel | ✓ |
| 44 | 40894464 | 20971520000 | 5 | 2 | channel | ✓ |
| 45 | 40894464 | 20971520000 | 6 | 1 | channel | ✓ |
| 46 | 40894464 | 52428800000 | 0 | 7 | channel | ✓ |
| 47 | 40894464 | 52428800000 | 1 | 1 | 32 | ✓ |
| 48 | 40894464 | 52428800000 | 1 | 1 | 64 | ✓ |
| 49 | 40894464 | 52428800000 | 1 | 1 | 128 | ✓ |
| 50 | 40894464 | 52428800000 | 1 | 1 | 256 | ✓ |
| 51 | 40894464 | 52428800000 | 1 | 1 | 512 | ✓ |
| 52 | 40894464 | 52428800000 | 1 | 1 | channel | ✓ |
| 53 | 40894464 | 52428800000 | 1 | 1 | tensor | ✓ |
| 54 | 40894464 | 52428800000 | 1 | 2 | channel | ✓ |
| 55 | 40894464 | 52428800000 | 1 | 3 | channel | ✓ |
| 56 | 40894464 | 52428800000 | 1 | 4 | channel | ✓ |
| 57 | 40894464 | 52428800000 | 1 | 5 | channel | ✓ |
| 58 | 40894464 | 52428800000 | 1 | 6 | channel | ✓ |
| 59 | 40894464 | 52428800000 | 2 | 1 | channel | ✓ |
| 60 | 40894464 | 52428800000 | 2 | 3 | channel | ✓ |
| 61 | 40894464 | 52428800000 | 3 | 1 | channel | ✓ |
| 62 | 40894464 | 52428800000 | 3 | 2 | channel | ✓ |
| 63 | 40894464 | 52428800000 | 4 | 1 | channel | ✓ |
| 64 | 40894464 | 52428800000 | 4 | 3 | channel | ✓ |
| 65 | 40894464 | 52428800000 | 4 | 5 | channel | ✓ |
| 66 | 40894464 | 52428800000 | 5 | 1 | channel | ✓ |
| 67 | 40894464 | 52428800000 | 5 | 2 | channel | ✓ |
| 68 | 40894464 | 52428800000 | 6 | 1 | channel | ✓ |
| 69 | 40894464 | 104857600000 | 0 | 7 | channel | ✓ |
| 70 | 40894464 | 104857600000 | 1 | 1 | 32 | ✓ |
| 71 | 40894464 | 104857600000 | 1 | 1 | 64 | ✓ |
| 72 | 40894464 | 104857600000 | 1 | 1 | 128 | ✓ |
| 73 | 40894464 | 104857600000 | 1 | 1 | 256 | ✓ |
| 74 | 40894464 | 104857600000 | 1 | 1 | 512 | ✓ |
| 75 | 40894464 | 104857600000 | 1 | 1 | channel | ✓ |
| 76 | 40894464 | 104857600000 | 1 | 1 | tensor | ✓ |
| 77 | 40894464 | 104857600000 | 1 | 2 | channel | ✓ |
| 78 | 40894464 | 104857600000 | 1 | 3 | channel | ✓ |
| 79 | 40894464 | 104857600000 | 1 | 4 | channel | ✓ |
| 80 | 40894464 | 104857600000 | 1 | 5 | channel | ✓ |
| 81 | 40894464 | 104857600000 | 1 | 6 | channel | ✓ |
| 82 | 40894464 | 104857600000 | 2 | 1 | channel | ✓ |
| 83 | 40894464 | 104857600000 | 2 | 3 | channel | ✓ |
| 84 | 40894464 | 104857600000 | 3 | 1 | channel | ✓ |
| 85 | 40894464 | 104857600000 | 3 | 2 | channel | ✓ |
| 86 | 40894464 | 104857600000 | 4 | 1 | channel | ✓ |
| 87 | 40894464 | 104857600000 | 4 | 3 | channel | ✓ |
| 88 | 40894464 | 104857600000 | 4 | 5 | channel | ✓ |
| 89 | 40894464 | 104857600000 | 5 | 1 | channel | ✓ |
| 90 | 40894464 | 104857600000 | 5 | 2 | channel | ✓ |
| 91 | 40894464 | 104857600000 | 6 | 1 | channel | ✓ |
| 92 | 84934656 | 10485760000 | 0 | 7 | channel | ✓ |
| 93 | 84934656 | 10485760000 | 1 | 1 | 32 | ✓ |
| 94 | 84934656 | 10485760000 | 1 | 1 | 64 | ✓ |
| 95 | 84934656 | 10485760000 | 1 | 1 | 128 | ✓ |
| 96 | 84934656 | 10485760000 | 1 | 1 | 256 | ✓ |
| 97 | 84934656 | 10485760000 | 1 | 1 | channel | ✓ |
| 98 | 84934656 | 10485760000 | 1 | 1 | tensor | ✓ |
| 99 | 84934656 | 10485760000 | 1 | 2 | channel | ✓ |
| 100 | 84934656 | 10485760000 | 1 | 3 | channel | ✓ |
| 101 | 84934656 | 10485760000 | 1 | 4 | channel | ✓ |
| 102 | 84934656 | 10485760000 | 1 | 5 | channel | ✓ |
| 103 | 84934656 | 10485760000 | 1 | 6 | channel | ✓ |
| 104 | 84934656 | 10485760000 | 2 | 1 | channel | ✓ |
| 105 | 84934656 | 10485760000 | 2 | 3 | channel | ✓ |
| 106 | 84934656 | 10485760000 | 3 | 1 | channel | ✓ |
| 107 | 84934656 | 10485760000 | 3 | 2 | channel | ✓ |
| 108 | 84934656 | 10485760000 | 4 | 1 | channel | ✓ |
| 109 | 84934656 | 10485760000 | 4 | 3 | channel | ✓ |
| 110 | 84934656 | 10485760000 | 4 | 5 | channel | ✓ |
| 111 | 84934656 | 10485760000 | 5 | 1 | channel | ✓ |
| 112 | 84934656 | 10485760000 | 5 | 2 | channel | ✓ |
| 113 | 84934656 | 10485760000 | 6 | 1 | channel | ✓ |
| 114 | 84934656 | 20971520000 | 0 | 7 | channel | ✓ |
| 115 | 84934656 | 20971520000 | 1 | 1 | 32 | ✓ |
| 116 | 84934656 | 20971520000 | 1 | 1 | 64 | ✓ |
| 117 | 84934656 | 20971520000 | 1 | 1 | 128 | ✓ |
| 118 | 84934656 | 20971520000 | 1 | 1 | 256 | ✓ |
| 119 | 84934656 | 20971520000 | 1 | 1 | channel | ✓ |
| 120 | 84934656 | 20971520000 | 1 | 1 | tensor | ✓ |
| 121 | 84934656 | 20971520000 | 1 | 2 | channel | ✓ |
| 122 | 84934656 | 20971520000 | 1 | 3 | channel | ✓ |
| 123 | 84934656 | 20971520000 | 1 | 4 | channel | ✓ |
| 124 | 84934656 | 20971520000 | 1 | 5 | channel | ✓ |
| 125 | 84934656 | 20971520000 | 1 | 6 | channel | ✓ |
| 126 | 84934656 | 20971520000 | 2 | 1 | channel | ✓ |
| 127 | 84934656 | 20971520000 | 2 | 3 | channel | ✓ |
| 128 | 84934656 | 20971520000 | 3 | 1 | channel | ✓ |
| 129 | 84934656 | 20971520000 | 3 | 2 | channel | ✓ |
| 130 | 84934656 | 20971520000 | 4 | 1 | channel | ✓ |
| 131 | 84934656 | 20971520000 | 4 | 3 | channel | ✓ |
| 132 | 84934656 | 20971520000 | 4 | 5 | channel | ✓ |
| 133 | 84934656 | 20971520000 | 5 | 1 | channel | ✓ |
| 134 | 84934656 | 20971520000 | 5 | 2 | channel | ✓ |
| 135 | 84934656 | 20971520000 | 6 | 1 | channel | ✓ |
| 136 | 84934656 | 52428800000 | 0 | 7 | channel | ✓ |
| 137 | 84934656 | 52428800000 | 1 | 1 | 32 | ✓ |
| 138 | 84934656 | 52428800000 | 1 | 1 | 64 | ✓ |
| 139 | 84934656 | 52428800000 | 1 | 1 | 128 | ✓ |
| 140 | 84934656 | 52428800000 | 1 | 1 | 256 | ✓ |
| 141 | 84934656 | 52428800000 | 1 | 1 | channel | ✓ |
| 142 | 84934656 | 52428800000 | 1 | 1 | tensor | ✓ |
| 143 | 84934656 | 52428800000 | 1 | 2 | channel | ✓ |
| 144 | 84934656 | 52428800000 | 1 | 3 | channel | ✓ |
| 145 | 84934656 | 52428800000 | 1 | 4 | channel | ✓ |
| 146 | 84934656 | 52428800000 | 1 | 5 | channel | ✓ |
| 147 | 84934656 | 52428800000 | 1 | 6 | channel | ✓ |
| 148 | 84934656 | 52428800000 | 2 | 1 | channel | ✓ |
| 149 | 84934656 | 52428800000 | 2 | 3 | channel | ✓ |
| 150 | 84934656 | 52428800000 | 3 | 1 | channel | ✓ |
| 151 | 84934656 | 52428800000 | 3 | 2 | channel | ✓ |
| 152 | 84934656 | 52428800000 | 4 | 1 | channel | ✓ |
| 153 | 84934656 | 52428800000 | 4 | 3 | channel | ✓ |
| 154 | 84934656 | 52428800000 | 4 | 5 | channel | ✓ |
| 155 | 84934656 | 52428800000 | 5 | 1 | channel | ✓ |
| 156 | 84934656 | 52428800000 | 5 | 2 | channel | ✓ |
| 157 | 84934656 | 52428800000 | 6 | 1 | channel | ✓ |
| 158 | 84934656 | 104857600000 | 0 | 7 | channel | ✓ |
| 159 | 84934656 | 104857600000 | 1 | 1 | 32 | ✓ |
| 160 | 84934656 | 104857600000 | 1 | 1 | 64 | ✓ |
| 161 | 84934656 | 104857600000 | 1 | 1 | 128 | ✓ |
| 162 | 84934656 | 104857600000 | 1 | 1 | 256 | ✓ |
| 163 | 84934656 | 104857600000 | 1 | 1 | channel | ✓ |
| 164 | 84934656 | 104857600000 | 1 | 1 | tensor | ✓ |
| 165 | 84934656 | 104857600000 | 1 | 2 | channel | ✓ |
| 166 | 84934656 | 104857600000 | 1 | 3 | channel | ✓ |
| 167 | 84934656 | 104857600000 | 1 | 4 | channel | ✓ |
| 168 | 84934656 | 104857600000 | 1 | 5 | channel | ✓ |
| 169 | 84934656 | 104857600000 | 1 | 6 | channel | ✓ |
| 170 | 84934656 | 104857600000 | 2 | 1 | channel | ✓ |
| 171 | 84934656 | 104857600000 | 2 | 3 | channel | ✓ |
| 172 | 84934656 | 104857600000 | 3 | 1 | channel | ✓ |
| 173 | 84934656 | 104857600000 | 3 | 2 | channel | ✓ |
| 174 | 84934656 | 104857600000 | 4 | 1 | channel | ✓ |
| 175 | 84934656 | 104857600000 | 4 | 3 | channel | ✓ |
| 176 | 84934656 | 104857600000 | 4 | 5 | channel | ✓ |
| 177 | 84934656 | 104857600000 | 5 | 1 | channel | ✓ |
| 178 | 84934656 | 104857600000 | 5 | 2 | channel | ✓ |
| 179 | 84934656 | 104857600000 | 6 | 1 | channel | ✓ |
| 180 | 154140672 | 10485760000 | 0 | 7 | channel | ✓ |
| 181 | 154140672 | 10485760000 | 1 | 1 | 32 | ✓ |
| 182 | 154140672 | 10485760000 | 1 | 1 | 64 | ✓ |
| 183 | 154140672 | 10485760000 | 1 | 1 | 128 | ✓ |
| 184 | 154140672 | 10485760000 | 1 | 1 | 256 | ✓ |
| 185 | 154140672 | 10485760000 | 1 | 1 | channel | ✓ |
| 186 | 154140672 | 10485760000 | 1 | 1 | tensor | ✓ |
| 187 | 154140672 | 10485760000 | 1 | 2 | channel | ✓ |
| 188 | 154140672 | 10485760000 | 1 | 3 | channel | ✓ |
| 189 | 154140672 | 10485760000 | 1 | 4 | channel | ✓ |
| 190 | 154140672 | 10485760000 | 1 | 5 | channel | ✓ |
| 191 | 154140672 | 10485760000 | 1 | 6 | channel | ✓ |
| 192 | 154140672 | 10485760000 | 2 | 1 | channel | ✓ |
| 193 | 154140672 | 10485760000 | 2 | 3 | channel | ✓ |
| 194 | 154140672 | 10485760000 | 3 | 1 | channel | ✓ |
| 195 | 154140672 | 10485760000 | 3 | 2 | channel | ✓ |
| 196 | 154140672 | 10485760000 | 4 | 1 | channel | ✓ |
| 197 | 154140672 | 10485760000 | 4 | 3 | channel | ✓ |
| 198 | 154140672 | 10485760000 | 4 | 5 | channel | ✓ |
| 199 | 154140672 | 10485760000 | 5 | 1 | channel | ✓ |
| 200 | 154140672 | 10485760000 | 5 | 2 | channel | ✓ |
| 201 | 154140672 | 10485760000 | 6 | 1 | channel | ✓ |
| 202 | 154140672 | 20971520000 | 0 | 7 | channel | ✓ |
| 203 | 154140672 | 20971520000 | 1 | 1 | 32 | ✓ |
| 204 | 154140672 | 20971520000 | 1 | 1 | 64 | ✓ |
| 205 | 154140672 | 20971520000 | 1 | 1 | 128 | ✓ |
| 206 | 154140672 | 20971520000 | 1 | 1 | 256 | ✓ |
| 207 | 154140672 | 20971520000 | 1 | 1 | channel | ✓ |
| 208 | 154140672 | 20971520000 | 1 | 1 | tensor | ✓ |
| 209 | 154140672 | 20971520000 | 1 | 2 | channel | ✓ |
| 210 | 154140672 | 20971520000 | 1 | 3 | channel | ✓ |
| 211 | 154140672 | 20971520000 | 1 | 4 | channel | ✓ |
| 212 | 154140672 | 20971520000 | 1 | 5 | channel | ✓ |
| 213 | 154140672 | 20971520000 | 1 | 6 | channel | ✓ |
| 214 | 154140672 | 20971520000 | 2 | 1 | channel | ✓ |
| 215 | 154140672 | 20971520000 | 2 | 3 | channel | ✓ |
| 216 | 154140672 | 20971520000 | 3 | 1 | channel | ✓ |
| 217 | 154140672 | 20971520000 | 3 | 2 | channel | ✓ |
| 218 | 154140672 | 20971520000 | 4 | 1 | channel | ✓ |
| 219 | 154140672 | 20971520000 | 4 | 3 | channel | ✓ |
| 220 | 154140672 | 20971520000 | 4 | 5 | channel | ✓ |
| 221 | 154140672 | 20971520000 | 5 | 1 | channel | ✓ |
| 222 | 154140672 | 20971520000 | 5 | 2 | channel | ✓ |
| 223 | 154140672 | 20971520000 | 6 | 1 | channel | ✓ |
| 224 | 154140672 | 52428800000 | 0 | 7 | channel | ✓ |
| 225 | 154140672 | 52428800000 | 1 | 1 | 32 | ✓ |
| 226 | 154140672 | 52428800000 | 1 | 1 | 64 | ✓ |
| 227 | 154140672 | 52428800000 | 1 | 1 | 128 | ✓ |
| 228 | 154140672 | 52428800000 | 1 | 1 | 256 | ✓ |
| 229 | 154140672 | 52428800000 | 1 | 1 | channel | ✓ |
| 230 | 154140672 | 52428800000 | 1 | 1 | tensor | ✓ |
| 231 | 154140672 | 52428800000 | 1 | 2 | channel | ✓ |
| 232 | 154140672 | 52428800000 | 1 | 3 | channel | ✓ |
| 233 | 154140672 | 52428800000 | 1 | 4 | channel | ✓ |
| 234 | 154140672 | 52428800000 | 1 | 5 | channel | ✓ |
| 235 | 154140672 | 52428800000 | 1 | 6 | channel | ✓ |
| 236 | 154140672 | 52428800000 | 2 | 1 | channel | ✓ |
| 237 | 154140672 | 52428800000 | 2 | 3 | channel | ✓ |
| 238 | 154140672 | 52428800000 | 3 | 1 | channel | ✓ |
| 239 | 154140672 | 52428800000 | 3 | 2 | channel | ✓ |
| 240 | 154140672 | 52428800000 | 4 | 1 | channel | ✓ |
| 241 | 154140672 | 52428800000 | 4 | 3 | channel | ✓ |
| 242 | 154140672 | 52428800000 | 4 | 5 | channel | ✓ |
| 243 | 154140672 | 52428800000 | 5 | 1 | channel | ✓ |
| 244 | 154140672 | 52428800000 | 5 | 2 | channel | ✓ |
| 245 | 154140672 | 52428800000 | 6 | 1 | channel | ✓ |
| 246 | 154140672 | 104857600000 | 0 | 7 | channel | ✓ |
| 247 | 154140672 | 104857600000 | 1 | 1 | 32 | ✓ |
| 248 | 154140672 | 104857600000 | 1 | 1 | 64 | ✓ |
| 249 | 154140672 | 104857600000 | 1 | 1 | 128 | ✓ |
| 250 | 154140672 | 104857600000 | 1 | 1 | 256 | ✓ |
| 251 | 154140672 | 104857600000 | 1 | 1 | channel | ✓ |
| 252 | 154140672 | 104857600000 | 1 | 1 | tensor | ✓ |
| 253 | 154140672 | 104857600000 | 1 | 2 | channel | ✓ |
| 254 | 154140672 | 104857600000 | 1 | 3 | channel | ✓ |
| 255 | 154140672 | 104857600000 | 1 | 4 | channel | ✓ |
| 256 | 154140672 | 104857600000 | 1 | 5 | channel | ✓ |
| 257 | 154140672 | 104857600000 | 1 | 6 | channel | ✓ |
| 258 | 154140672 | 104857600000 | 2 | 1 | channel | ✓ |
| 259 | 154140672 | 104857600000 | 2 | 3 | channel | ✓ |
| 260 | 154140672 | 104857600000 | 3 | 1 | channel | ✓ |
| 261 | 154140672 | 104857600000 | 3 | 2 | channel | ✓ |
| 262 | 154140672 | 104857600000 | 4 | 1 | channel | ✓ |
| 263 | 154140672 | 104857600000 | 4 | 3 | channel | ✓ |
| 264 | 154140672 | 104857600000 | 4 | 5 | channel | ✓ |
| 265 | 154140672 | 104857600000 | 5 | 1 | channel | ✓ |
| 266 | 154140672 | 104857600000 | 5 | 2 | channel | ✓ |
| 267 | 154140672 | 104857600000 | 6 | 1 | channel | ✓ |
| 268 | 679477248 | 10485760000 | 0 | 7 | channel | ✓ |
| 269 | 679477248 | 10485760000 | 1 | 1 | 32 | ✓ |
| 270 | 679477248 | 10485760000 | 1 | 1 | 64 | ✓ |
| 271 | 679477248 | 10485760000 | 1 | 1 | 128 | ✓ |
| 272 | 679477248 | 10485760000 | 1 | 1 | 256 | ✓ |
| 273 | 679477248 | 10485760000 | 1 | 1 | 512 | ✓ |
| 274 | 679477248 | 10485760000 | 1 | 1 | channel | ✓ |
| 275 | 679477248 | 10485760000 | 1 | 1 | tensor | ✓ |
| 276 | 679477248 | 10485760000 | 1 | 2 | channel | ✓ |
| 277 | 679477248 | 10485760000 | 1 | 3 | channel | ✓ |
| 278 | 679477248 | 10485760000 | 1 | 4 | channel | ✓ |
| 279 | 679477248 | 10485760000 | 1 | 5 | channel | ✓ |
| 280 | 679477248 | 10485760000 | 1 | 6 | channel | ✓ |
| 281 | 679477248 | 10485760000 | 2 | 1 | channel | ✓ |
| 282 | 679477248 | 10485760000 | 2 | 3 | channel | ✓ |
| 283 | 679477248 | 10485760000 | 3 | 1 | channel | ✓ |
| 284 | 679477248 | 10485760000 | 3 | 2 | channel | ✓ |
| 285 | 679477248 | 10485760000 | 4 | 1 | channel | ✓ |
| 286 | 679477248 | 10485760000 | 4 | 3 | channel | ✓ |
| 287 | 679477248 | 10485760000 | 4 | 5 | channel | ✓ |
| 288 | 679477248 | 10485760000 | 5 | 1 | channel | ✓ |
| 289 | 679477248 | 10485760000 | 5 | 2 | channel | ✓ |
| 290 | 679477248 | 10485760000 | 6 | 1 | channel | ✓ |
| 291 | 679477248 | 20971520000 | 0 | 7 | channel | ✓ |
| 292 | 679477248 | 20971520000 | 1 | 1 | 32 | ✓ |
| 293 | 679477248 | 20971520000 | 1 | 1 | 64 | ✓ |
| 294 | 679477248 | 20971520000 | 1 | 1 | 128 | ✓ |
| 295 | 679477248 | 20971520000 | 1 | 1 | 256 | ✓ |
| 296 | 679477248 | 20971520000 | 1 | 1 | 512 | ✓ |
| 297 | 679477248 | 20971520000 | 1 | 1 | channel | ✓ |
| 298 | 679477248 | 20971520000 | 1 | 1 | tensor | ✓ |
| 299 | 679477248 | 20971520000 | 1 | 2 | channel | ✓ |
| 300 | 679477248 | 20971520000 | 1 | 3 | channel | ✓ |
| 301 | 679477248 | 20971520000 | 1 | 4 | channel | ✓ |
| 302 | 679477248 | 20971520000 | 1 | 5 | channel | ✓ |
| 303 | 679477248 | 20971520000 | 1 | 6 | channel | ✓ |
| 304 | 679477248 | 20971520000 | 2 | 1 | channel | ✓ |
| 305 | 679477248 | 20971520000 | 2 | 3 | channel | ✓ |
| 306 | 679477248 | 20971520000 | 3 | 1 | channel | ✓ |
| 307 | 679477248 | 20971520000 | 3 | 2 | channel | ✓ |
| 308 | 679477248 | 20971520000 | 4 | 1 | channel | ✓ |
| 309 | 679477248 | 20971520000 | 4 | 3 | channel | ✓ |
| 310 | 679477248 | 20971520000 | 4 | 5 | channel | ✓ |
| 311 | 679477248 | 20971520000 | 5 | 1 | channel | ✓ |
| 312 | 679477248 | 20971520000 | 5 | 2 | channel | ✓ |
| 313 | 679477248 | 20971520000 | 6 | 1 | channel | ✓ |
| 314 | 679477248 | 52428800000 | 0 | 7 | channel | ✓ |
| 315 | 679477248 | 52428800000 | 1 | 1 | 32 | ✓ |
| 316 | 679477248 | 52428800000 | 1 | 1 | 64 | ✓ |
| 317 | 679477248 | 52428800000 | 1 | 1 | 128 | ✓ |
| 318 | 679477248 | 52428800000 | 1 | 1 | 256 | ✓ |
| 319 | 679477248 | 52428800000 | 1 | 1 | 512 | ✓ |
| 320 | 679477248 | 52428800000 | 1 | 1 | channel | ✓ |
| 321 | 679477248 | 52428800000 | 1 | 1 | tensor | ✓ |
| 322 | 679477248 | 52428800000 | 1 | 2 | channel | ✓ |
| 323 | 679477248 | 52428800000 | 1 | 3 | channel | ✓ |
| 324 | 679477248 | 52428800000 | 1 | 4 | channel | ✓ |
| 325 | 679477248 | 52428800000 | 1 | 5 | channel | ✓ |
| 326 | 679477248 | 52428800000 | 1 | 6 | channel | ✓ |
| 327 | 679477248 | 52428800000 | 2 | 1 | channel | ✓ |
| 328 | 679477248 | 52428800000 | 2 | 3 | channel | ✓ |
| 329 | 679477248 | 52428800000 | 3 | 1 | channel | ✓ |
| 330 | 679477248 | 52428800000 | 3 | 2 | channel | ✓ |
| 331 | 679477248 | 52428800000 | 4 | 1 | channel | ✓ |
| 332 | 679477248 | 52428800000 | 4 | 3 | channel | ✓ |
| 333 | 679477248 | 52428800000 | 4 | 5 | channel | ✓ |
| 334 | 679477248 | 52428800000 | 5 | 1 | channel | ✓ |
| 335 | 679477248 | 52428800000 | 5 | 2 | channel | ✓ |
| 336 | 679477248 | 52428800000 | 6 | 1 | channel | ✓ |
| 337 | 679477248 | 104857600000 | 0 | 7 | channel | ✓ |
| 338 | 679477248 | 104857600000 | 1 | 1 | 32 | ✓ |
| 339 | 679477248 | 104857600000 | 1 | 1 | 64 | ✓ |
| 340 | 679477248 | 104857600000 | 1 | 1 | 128 | ✓ |
| 341 | 679477248 | 104857600000 | 1 | 1 | 256 | ✓ |
| 342 | 679477248 | 104857600000 | 1 | 1 | 512 | ✓ |
| 343 | 679477248 | 104857600000 | 1 | 1 | channel | ✓ |
| 344 | 679477248 | 104857600000 | 1 | 1 | tensor | ✓ |
| 345 | 679477248 | 104857600000 | 1 | 2 | channel | ✓ |
| 346 | 679477248 | 104857600000 | 1 | 3 | channel | ✓ |
| 347 | 679477248 | 104857600000 | 1 | 4 | channel | ✓ |
| 348 | 679477248 | 104857600000 | 1 | 5 | channel | ✓ |
| 349 | 679477248 | 104857600000 | 1 | 6 | channel | ✓ |
| 350 | 679477248 | 104857600000 | 2 | 1 | channel | ✓ |
| 351 | 679477248 | 104857600000 | 2 | 3 | channel | ✓ |
| 352 | 679477248 | 104857600000 | 3 | 1 | channel | ✓ |
| 353 | 679477248 | 104857600000 | 3 | 2 | channel | ✓ |
| 354 | 679477248 | 104857600000 | 4 | 1 | channel | ✓ |
| 355 | 679477248 | 104857600000 | 4 | 3 | channel | ✓ |
| 356 | 679477248 | 104857600000 | 4 | 5 | channel | ✓ |
| 357 | 679477248 | 104857600000 | 5 | 2 | channel | ✓ |
| 358 | 679477248 | 104857600000 | 6 | 1 | channel | ✓ |
| 359 | 1233125376 | 10485760000 | 1 | 2 | 512 | ✗ |
| 360 | 1233125376 | 10485760000 | 4 | 3 | 512 | ✗ |
| 361 | 1233125376 | 20971520000 | 1 | 2 | 512 | ✗ |
| 362 | 1233125376 | 20971520000 | 4 | 3 | 512 | ✗ |
| 363 | 1233125376 | 52428800000 | 1 | 2 | 512 | ✗ |
| 364 | 1233125376 | 52428800000 | 4 | 3 | 512 | ✗ |
| 365 | 1233125376 | 104857600000 | 1 | 2 | 512 | ✗ |
| 366 | 1233125376 | 104857600000 | 4 | 3 | 512 | ✗ |
🔼 표 3은 본 논문의 실험적 분석을 위한 모든 설정값을 보여줍니다. 각 행은 모델 크기(N), 데이터 크기(D), 지수 비트(E), 가수 비트(M), 스케일링 팩터 블록 크기(B), 그리고 해당 설정이 실험에 사용되었는지 여부를 나타냅니다. 이 표는 본 논문의 ablation study에 사용된 다양한 모델과 훈련 설정에 대한 포괄적인 개요를 제공합니다. 여러 변수를 조합하여 실험을 진행했는지 확인하는 데 도움이 됩니다.
read the caption
Table 3: All configurations for the ablation experiments.
Full paper#



















