↗ arXiv ↗ Hugging Face ↗ Papers with Code
TL;DR#
기존 그래프 생성 모델들은 인접 행렬을 사용하여 그래프를 표현하는데, 이는 복잡한 그래프의 효율적인 인코딩과 생성에 어려움을 초래합니다. 또한, 대부분의 기존 모델들은 그래프의 순서를 고려하지 않아, 실제 그래프의 순차적 특징을 제대로 반영하지 못하는 한계가 있습니다. 본 논문에서는 이러한 문제를 해결하기 위해 새로운 접근 방식을 제안합니다.
본 논문에서는 그래프를 노드와 엣지의 시퀀스로 표현하는 새로운 방법을 제시하고, 자동 회귀 모델인 Transformer 디코더를 이용한 G2PT 모델을 개발했습니다. G2PT는 다음 토큰 예측을 통해 그래프 구조를 학습하며, 목표 지향적 생성 및 그래프 속성 예측과 같은 다운스트림 작업에도 효과적으로 적용될 수 있습니다. 실험 결과, G2PT는 다양한 그래프 생성 및 예측 작업에서 기존 최고 성능 모델들을 능가하는 결과를 보였습니다. 이는 제시된 새로운 표현 방식과 G2PT 모델의 우수성을 입증하는 것입니다.
Key Takeaways#
Why does it matter?#
본 논문은 그래프 생성 모델링 분야의 새로운 접근법을 제시하여, 기존 방식의 한계를 극복하고 성능을 향상시켰다는 점에서 큰 의의가 있습니다. 대규모 언어 모델의 성공에 착안하여 그래프를 시퀀스로 표현하고 Transformer 디코더를 활용한 새로운 모델(G2PT)을 제안하여, 다양한 그래프 생성 및 예측 작업에서 우수한 성능을 달성하였습니다. 목표 지향적 생성 및 그래프 특성 예측과 같은 다운스트림 작업에도 적용 가능성을 보여줌으로써, 향후 연구의 새로운 방향을 제시하고 있습니다. 특히, 효율적인 그래프 인코딩 방식과 다운스트림 작업에 대한 적응력은 다른 연구자들에게 큰 영감을 줄 수 있습니다.
Visual Insights#

🔼 그림 1은 본 논문에서 제안하는 그래프 시퀀스 표현 방식을 보여줍니다. 이 방식은 그래프 생성 과정을 일련의 행위들로 나타내는데, 먼저 모든 노드(노드 타입, 노드 인덱스)를 생성한 후, 각 단계마다 명시적으로 간선(출발 노드 인덱스, 도착 노드 인덱스, 간선 타입)을 추가하는 방식입니다. 모든 행위들은 통합된 어휘집에 매핑되어 단일 토큰 공간을 사용합니다. 이를 통해 그래프 생성 과정을 효율적이고 체계적으로 표현하며, 변환기 모델이 시퀀스 데이터를 처리하는 데 적합하게 만듭니다. 다시 말해, 그래프를 노드와 에지의 시퀀스로 나타내고, 이 시퀀스를 변환기 모델의 입력으로 사용하여 그래프를 생성하는 방식입니다.
read the caption
Figure 1: Illustration of our proposed graph sequence representation. This representation can be viewed as a sequence of actions: first generating all nodes (node type, node index), then explicitly adding edges (source node index, destination node index, edge type) step by step until completion. A unified vocabulary is used to map different types of actions into a shared token space.
| Model (Rep.) | Likelihood | Illustration | #Network Calls | #Variables | Decomposition |
|---|---|---|---|---|---|
| Diffusion (A) | p(AT)∏t=1Tp(At-1 | At) | https://arxiv.org/html/2501.01073/x1.png | T | O(Tn2) |
| Auto-regressive (A) | ∏i=2n∏j=1i-1p(Ai,j | A<i,<i-1,Ai,<j) | https://arxiv.org/html/2501.01073/x2.png | O(n2) | O(n2) |
| Auto-regressive (E) | p(e1)∏i=2mp(ei | e<i) | https://arxiv.org/html/2501.01073/x3.png | O(m) | O(m) |
🔼 표 1은 그래프 생성 모델의 종류와 사용된 데이터 표현 방식(Rep.)을 보여줍니다. n은 노드의 개수, m은 에지의 개수를 나타냅니다. 그림에서 실선은 에지를, 점선은 비에지를 나타내며, 현재 단계에서 생성된 (비)에지는 파란색으로 표시됩니다. 제안된 G2PT 모델은 에지 집합(E)을 이용하여 학습하는 자기 회귀 모델입니다.
read the caption
Table 1: Overview of graph generative model families combined with the used data representation (Rep.). n𝑛nitalic_n: number of nodes. m𝑚mitalic_m: number of edges. In the illustration, we use solid line for edges and dash line for non-edges, (non-)edges generated at current step are colored in blue. Our proposed G2PT is an Auto-regressive model that learns on E𝐸Eitalic_E representation.
In-depth insights#
GraphSeq: A Novel Approach#
GraphSeq는 그래프 데이터를 효율적으로 인코딩하는 새로운 시퀀스 기반 표현 방법을 제안하는 혁신적인 접근 방식입니다. 기존의 인접 행렬 방식과 달리, GraphSeq는 그래프를 노드와 엣지의 시퀀스로 표현하여 메모리 효율성을 높이고, 그래프의 구조적 특징을 보다 효과적으로 포착합니다. 이러한 시퀀스 표현은 트랜스포머 디코더와 같은 순차적 모델을 사용하여 그래프 생성 작업에 적용될 수 있으며, 자연어 처리 분야에서 성공적으로 사용된 트랜스포머의 강력한 표현 능력을 그래프 생성 문제에 적용하는 데 기여합니다. GraphSeq는 다양한 그래프 생성 작업과 그래프 특징 예측 작업에서 우수한 성능을 보여주는 것으로 실험 결과를 통해 입증되었습니다. 또한, GraphSeq는 목표 지향적 생성 및 그래프 속성 예측과 같은 다운스트림 작업에 쉽게 적용될 수 있어 범용적인 기반 모델로서의 가능성을 제시합니다. GraphSeq의 핵심은 그래프의 효율적인 인코딩과 트랜스포머 디코더의 강력한 표현 능력을 결합하여 그래프 생성 문제에 대한 새로운 해결책을 제시하는 데 있습니다.
G2PT: Transformer Decoder#
본 논문에서 제시된 G2PT(Graph Generative Pre-trained Transformer)의 Transformer Decoder는 그래프를 시퀀스로 표현하여 자동 회귀 방식으로 그래프를 생성하는 모델의 핵심 구성 요소입니다. 기존의 그래프 생성 모델들이 인접 행렬을 사용하는 것과 달리, G2PT는 노드와 에지 정보를 시퀀스 형태로 변환하여 Transformer Decoder에 입력합니다. 이를 통해 그래프의 구조적 정보를 효율적으로 인코딩하고, 다음 토큰 예측을 통해 그래프 생성을 수행합니다. Transformer Decoder는 자체적으로 사전 훈련되어 일반적인 그래프 구조 학습을 수행하고, 이후 **다운스트림 작업(목표 지향적 생성, 그래프 속성 예측)**에 미세 조정을 통해 특정 그래프 생성 또는 예측 작업에 효과적으로 적용될 수 있다는 점이 중요한 특징입니다. 자동 회귀 모델의 장점과 Transformer의 강력한 시퀀스 모델링 능력을 결합한 G2PT의 Transformer Decoder는 그래프 생성 분야에서 새로운 가능성을 제시합니다.
Fine-Tuning Strategies#
본 논문에서 제시된 “미세조정 전략"은 목표지향적 생성과 그래프 특징 예측이라는 두 가지 하위 작업에 초점을 맞춥니다. 목표지향적 생성을 위해 거절 샘플링 미세조정과 강화 학습 기법을 활용하여 특정 속성을 가진 그래프의 생성 확률을 높였습니다. 특히, 거절 샘플링 미세조정은 목표 속성을 만족하는 그래프만을 선택적으로 사용함으로써 효율성을 높였고, 강화 학습은 목표 속성 달성에 대한 보상을 통해 학습 과정을 유도했습니다. 그래프 특징 예측을 위해서는 사전 학습된 파라미터를 특정 작업에 맞춰 미세 조정하는 방식을 사용했으며, 이는 지도 학습 방식을 통해 그래프의 특징과 목표 변수 간의 관계를 학습하도록 했습니다. 두 가지 접근 방식 모두 사전 학습된 모델을 기반으로 하므로 효율적인 미세 조정이 가능하고, 다양한 하위 작업에 대한 적응력을 높였습니다. 전반적으로, 본 논문의 미세조정 전략은 다양한 그래프 생성 및 예측 작업에 효과적으로 적용될 수 있는 유연하고 강력한 접근 방식을 제시합니다.
Generative Performance#
본 논문에서 제시된 G2PT 모델의 생성 성능은 다양한 벤치마크 데이터셋에서 상당히 우수한 결과를 보여줍니다. 특히, 일반적인 그래프 생성 작업과 분자 생성 작업 모두에서 기존 최첨단 모델을 능가하거나 비슷한 수준의 성능을 달성했습니다. 이는 G2PT가 제안하는 새로운 그래프 표현 방식과 트랜스포머 디코더 기반의 자기회귀 모델 설계가 그래프 구조를 효과적으로 학습하고 생성하는 데 효과적임을 시사합니다. 다양한 하위 작업에 대한 미세 조정 전략 또한 생성 성능 향상에 크게 기여했습니다. 목표 지향적인 생성과 그래프 특징 예측 모두에서 뛰어난 적응력과 다양성을 보였습니다. 모델 크기 및 데이터 크기의 확장성을 분석한 결과, 모델 성능이 일정 수준까지 향상되다가 포화되는 경향을 보였으며, 데이터 다양성이 모델 성능 향상에 중요한 역할을 한다는 점도 확인했습니다. 전체적으로 G2PT는 그래프 생성 분야에서 강력하고 유연한 기반 모델임을 입증하였습니다.
Future Research#
본 논문에서 제시된 G2PT 모델은 그래프 생성 분야에 중요한 발전을 가져왔지만, 향후 연구를 위한 잠재력은 여전히 풍부합니다. 먼저, 다양한 그래프 구조에 대한 적응력 향상이 필요합니다. 현재 G2PT는 특정 유형의 그래프에 대해서는 뛰어난 성능을 보이지만, 다른 유형의 그래프에는 일반화가 어려울 수 있습니다. 따라서 더욱 다양하고 복잡한 그래프 구조를 생성할 수 있도록 모델 아키텍처와 학습 전략을 개선하는 연구가 필요합니다. 또한, 목표 지향적 그래프 생성의 효율성을 높이기 위한 연구가 중요합니다. 현재 논문에서 제시된 방법은 목표 함수를 달성하기 위해 반복적인 샘플링과 미세 조정을 필요로 하는데, 이는 계산 비용이 많이 들 수 있습니다. 더욱 효율적인 방법을 개발하여, 시간 및 자원을 절약하면서 원하는 특징을 가진 그래프를 생성하는 연구가 필요합니다. 마지막으로, 다른 머신 러닝 모델과의 통합을 통해 G2PT의 활용성을 더욱 확장하는 연구도 중요합니다. G2PT를 기반으로 다른 모델들과의 협업을 통해 그래프 데이터 분석 및 응용의 새로운 가능성을 제시할 수 있을 것입니다. 특히, 대규모 그래프 데이터에 대한 효율적인 학습 및 생성 방법에 대한 연구는 G2PT의 실제 응용 범위를 넓히는 데 중요한 역할을 할 것입니다.
More visual insights#
More on tables
| Planar | Tree | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Model | Deg. ↓ | Clus. ↓ | Orbit ↓ | Spec. ↓ | Wavelet ↓ | V.U.N. ↑ | Deg. ↓ | Clus. ↓ | Orbit ↓ | Spec. ↓ | Wavelet ↓ | V.U.N. ↑ |
| GRAN (Liao et al., 2019) | 7e-4 | 4.3e-2 | 9e-4 | 7.5e-3 | 1.9e-3 | 0 | 1.9e-1 | 8e-3 | 2e-2 | 2.8e-1 | 3.3e-1 | 0 |
| BiGG (Dai et al., 2020) | 7e-4 | 5.7e-2 | 3.7e-2 | 1.1e-2 | 5.2e-3 | 5 | 1.4e-3 | 0.00 | 0.00 | 1.2e-2 | 5.8e-3 | 75 |
| DiGress (Vignac et al., 2022) | 7e-4 | 7.8e-2 | 7.9e-3 | 9.8e-3 | 3.1e-3 | 77.5 | 2e-4 | 0.00 | 0.00 | 1.1e-2 | 4.3e-3 | 90 |
| BwR (Diamant et al., 2023) | 2.3e-2 | 2.6e-1 | 5.5e-1 | 4.4e-2 | 1.3e-1 | 0 | 1.6e-3 | 1.2e-1 | 3e-4 | 4.8e-2 | 3.9e-2 | 0 |
| HSpectre (Bergmeister et al., 2023) | 5e-4 | 6.3e-2 | 1.7e-3 | 7.5e-3 | 1.3e-3 | 95 | 1e-4 | 0.00 | 0.00 | 1.2e-2 | 4.7e-3 | 100 |
| DeFoG (Qin et al., 2024) | 5e-4 | 5e-2 | 6e-4 | 7.2e-3 | 1.4e-3 | 99.5 | 2e-4 | 0.00 | 0.00 | 1.1e-2 | 4.6e-3 | 96.5 |
| G2PTsmall | 4.7e-3 | 2.4e-3 | 0.00 | 1.6e-2 | 1.4e-2 | 95 | 2e-3 | 0.00 | 0.00 | 7.4e-3 | 3.9e-3 | 99 |
| G2PTbase | 1.8e-3 | 4.7e-3 | 0.00 | 8.1e-3 | 5.1e-3 | 100 | 4.3e-3 | 0.00 | 1e-4 | 7.3e-3 | 5.7e-3 | 99 |
| Lobster | SBM | |||||||||||
| — | — | — | — | — | — | — | — | — | — | — | — | — |
| Model | Deg. ↓ | Clus. ↓ | Orbit ↓ | Spec. ↓ | Wavelet ↓ | V.U.N. ↑ | Deg. ↓ | Clus. ↓ | Orbit ↓ | Spec. ↓ | Wavelet ↓ | V.U.N. ↑ |
| GRAN (Liao et al., 2019) | 3.8e-2 | 0.00 | 1e-3 | 2.7e-2 | - | - | 1.1e-2 | 5.5e-2 | 5.4e-2 | 5.4e-3 | 2.1e-2 | 25 |
| BiGG (Dai et al., 2020) | 0.00 | 0.00 | 0.00 | 9e-3 | - | - | 1.2e-3 | 6.0e-2 | 6.7e-2 | 5.9e-3 | 3.7e-2 | 10 |
| DiGress (Vignac et al., 2022) | 2.1e-2 | 0.00 | 4e-3 | - | - | - | 1.8e-3 | 4.9e-2 | 4.2e-2 | 4.5e-3 | 1.4e-3 | 60 |
| BwR (Diamant et al., 2023) | 3.2e-1 | 0.00 | 2.5e-1 | - | - | - | 4.8e-2 | 6.4e-2 | 1.1e-1 | 1.7e-2 | 8.9e-2 | 7.5 |
| HSpectre (Bergmeister et al., 2023) | - | - | - | - | - | - | 1.2e-2 | 5.2e-2 | 6.7e-2 | 6.7e-3 | 2.2e-2 | 45 |
| DeFoG (Qin et al., 2024) | - | - | - | - | - | - | 6e-4 | 5.2e-2 | 5.6e-2 | 5.4e-3 | 8e-3 | 90 |
| G2PTsmall | 2e-3 | 0.00 | 0.00 | 5e-3 | 8.5e-3 | 100 | 3.5e-3 | 1.2e-2 | 7e-4 | 7.6e-3 | 9.8e-3 | 100 |
| G2PTbase | 1e-3 | 0.00 | 0.00 | 4e-3 | 1e-2 | 100 | 4.2e-3 | 5.3e-3 | 3e-4 | 6.1e-3 | 6.9e-3 | 100 |
🔼 표 2는 일반적인 그래프 데이터셋에 대한 그래프 생성 성능을 보여줍니다. 다양한 그래프 생성 모델들의 성능을 Maximum Mean Discrepancy (MMD)를 사용하여 평가하였으며, Degree, Clustering Coefficient, Orbit Counts, Spectral Properties, Wavelet Statistics, 그리고 Valid, Unique, Novel samples 비율 등 다양한 지표를 통해 모델들의 생성 품질을 종합적으로 비교 분석했습니다. G2PT 모델의 우수한 성능을 확인할 수 있습니다.
read the caption
Table 2: Generative performance on generic graph datasets.
| Rep. | #Tokens ↓ | Deg. ↓ | Clus. ↓ | Orbit ↓ | Spec. ↓ | Wavelet ↓ | V.U.N. ↑ |
|---|---|---|---|---|---|---|---|
| 𝐀 | 2018 | 8.6e-3 | 1e-1 | 8e-3 | 3.2e-2 | 6.1e-2 | 94 |
| Ours | 737 | 4.7e-3 | 2.4e-3 | 0.00 | 1.6e-2 | 1.4e-2 | 95 |
🔼 본 표는 제안된 새로운 에지 시퀀스 표현 방식과 기존의 인접 행렬 표현 방식을 비교하여 그래프 생성 성능을 평가한 결과를 보여줍니다. 평가 지표는 다양한 그래프의 위상적 특징(토폴로지)을 포착하는 능력을 측정하며, 에지 시퀀스 표현 방식의 우수성을 보여줍니다. 특히, 제안된 방식은 더 적은 토큰 수로도 기존 방식보다 더 나은 성능을 보여주는 것을 확인할 수 있습니다.
read the caption
Table 3: Generative performance comparison between the proposed edge sequence and adjacency matrix representations.
| A | A | Ours | Ours |
|---|---|---|---|
 |  |  |  |
🔼 표 4는 다양한 분자 그래프 데이터셋에서 제안된 G2PT 모델의 생성 성능을 보여줍니다. 세부적으로는 MOSES, GuacaMol, QM9 데이터셋에서 G2PT 모델의 유효성, 고유성, 참신성, 필터링 통과율, FCD, SNN, Scaf 지표를 평가하여 기존의 최첨단 모델들과 비교 분석합니다. 각 지표는 분자 그래프 생성 모델의 성능을 다각적으로 평가하는 지표들로, 유효성은 생성된 분자들이 화학적으로 타당한지, 고유성은 생성된 분자들이 서로 다른지를, 참신성은 생성된 분자들이 기존 데이터셋에 존재하지 않는 새로운 분자인지를 나타냅니다. FCD와 SNN은 생성된 분자와 기존 분자들 사이의 유사성을 측정하는 지표이며, Scaf는 생성된 분자들의 골격 구조의 유사성을 측정하는 지표입니다. 표를 통해 G2PT 모델이 기존 모델들에 비해 우수한 성능을 보임을 확인할 수 있습니다.
read the caption
Table 4: Generative performance on molecular graph datasets
| Model | MOSES Validity ↑ | MOSES Unique. ↑ | MOSES Novelty ↑ | MOSES Filters ↑ | MOSES FCD ↓ | MOSES SNN ↑ | MOSES Scaf ↑ | GuacaMol Validity ↑ | GuacaMol Unique. ↑ | GuacaMol Novelty ↑ | GuacaMol KL Div. ↑ | GuacaMol FCD ↑ |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| DiGress (Vignac et al., 2022) | 85.7 | 100 | 95.0 | 97.1 | 1.19 | 0.52 | 14.8 | 85.2 | 100 | 99.9 | 92.9 | 68 |
| DisCo (Xu et al., 2024) | 88.3 | 100 | 97.7 | 95.6 | 1.44 | 0.5 | 15.1 | 86.6 | 86.6 | 86.5 | 92.6 | 59.7 |
| Cometh (Siraudin et al., 2024) | 90.5 | 99.9 | 92.6 | 99.1 | 1.27 | 0.54 | 16.0 | 98.9 | 98.9 | 97.6 | 96.7 | 72.7 |
| DeFoG (Qin et al., 2024) | 92.8 | 99.9 | 92.1 | 99.9 | 1.95 | 0.55 | 14.4 | 99.0 | 99.0 | 97.9 | 97.9 | 73.8 |
| G2PTsmall | 95.1 | 100 | 91.7 | 97.4 | 1.10 | 0.52 | 5.0 | 90.4 | 100 | 99.8 | 92.8 | 86.6 |
| G2PTbase | 96.4 | 100 | 86.0 | 98.3 | 0.97 | 0.55 | 3.3 | 94.6 | 100 | 99.5 | 96.0 | 93.4 |
| G2PTlarge | 97.2 | 100 | 79.4 | 98.9 | 1.02 | 0.55 | 2.9 | 95.3 | 100 | 99.5 | 95.6 | 92.7 |
🔼 표 5는 분자 특성 예측에 대한 ROC-AUC 결과를 보여줍니다. 세 번의 실행에 대한 평균과 표준 편차를 보고합니다. 여러 머신러닝 모델들의 성능을 비교하여 G2PT 모델의 효과성을 보여줍니다. 각 모델은 다양한 분자 특성 예측 작업(BBBP, Tox21, ToxCast, SIDER, ClinTox, MUV, HIV, BACE)에서 성능을 평가받습니다. 이 표는 각 작업에서의 ROC-AUC 값(평균 및 표준편차 포함)을 보여주어 G2PT 모델의 전반적인 성능을 평가하는 데 도움이 됩니다.
read the caption
Table 5: Results for molecule property prediction in terms of ROC-AUC. We report mean and standard deviation over three runs.
| Model | QM9 | ||
|---|---|---|---|
| Validity ↑ | Unique ↑ | FCD ↓ | |
| DiGress (Vignac et al., 2022) | 99.0 | 96.2 | - |
| DisCo (Xu et al., 2024) | 99.6 | 96.2 | 0.25 |
| Cometh (Siraudin et al., 2024) | 99.2 | 96.7 | 0.11 |
| DeFoG (Qin et al., 2024) | 99.3 | 96.3 | 0.12 |
| G2PTsmall | 99.0 | 96.7 | 0.06 |
| G2PTbase | 99.0 | 96.8 | 0.06 |
| G2PTlarge | 98.9 | 96.7 | 0.06 |
🔼 표 6은 논문에서 사용된 데이터셋의 통계를 요약한 표입니다. 각 데이터셋에 대한 노드 유형 수, 에지 유형 수, 노드 수의 평균 및 최대/최소값, 학습에 사용된 시퀀스 수, 어휘 크기, 최대 시퀀스 길이 등의 정보를 보여줍니다. 이 표는 다양한 크기와 복잡성의 그래프를 포함하는 데이터셋을 사용하여 실험을 수행했음을 보여줍니다.
read the caption
Table 6: Dataset statistics.
| MOSES | GuacaMol | |||||
|---|---|---|---|---|---|---|
| Train | G2PTsmall | G2PTbase | Train | G2PTsmall | G2PTbase | |
 |  |  |  |  |  | |
 |  |  |  |  |  |
🔼 표 7은 그래프 생성 사전 훈련에 사용된 하이퍼파라미터들을 보여줍니다. 모델 아키텍처(레이어 수, 헤드 수, dmodel), 최적화기(AdamW), 학습률 스케줄러(Cosine), 가중치 감쇠, 반복 횟수, 배치 크기, 그래디언트 누적, 그래디언트 클리핑 값, 웜업 반복 횟수 등의 세부 하이퍼파라미터 값들이 모델 크기별(10M, 85M, 300M 파라미터)로 제시되어 있습니다. 이 표는 모델 학습 과정에 대한 구체적인 설정 정보를 제공하여 재현성을 높이는 데 기여합니다.
read the caption
Table 7: Hyperparameters for graph generative pre-training.
| Density | QED Score | SA Score | GSK3β Score |
|---|---|---|---|
 |  |  | |
| (a) Rejection sampling fine-tuning (with self-bootstrap) | |||
| Density | QED Score | SA Score | GSK3β Score |
| — | — | — | — |
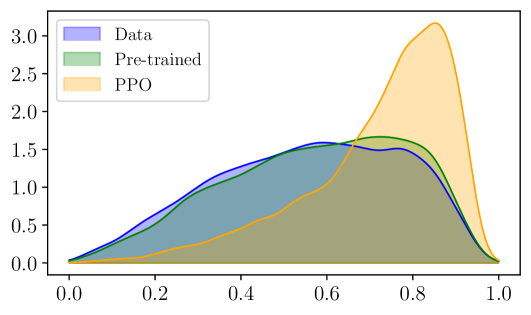 |  |  | |
| (b) Reinforcement learning framework (PPO) |
🔼 표 8은 강화 학습 알고리즘 중 하나인 근접 정책 최적화(PPO)를 사용하여 목표 지향적 분자 생성을 위한 미세 조정 과정에서 사용된 하이퍼파라미터들을 보여줍니다. 표에는 QED, SA, GSK3β 세 가지 속성에 대한 하이퍼파라미터 값들이 각각 나열되어 있으며, 보상 정규화 및 클리핑, 비율 클리핑, 엔트로피 정규화, 그레이디언트 클리핑 값, 학습률, 반복 횟수, 배치 크기 등의 세부 설정 값들이 포함되어 있습니다. 각 속성별로 최적의 성능을 얻기 위한 하이퍼파라미터 조정 결과를 확인할 수 있습니다.
read the caption
Table 8: Hyperparameters used for PPO training.
| BBBP | Tox21 | ToxCast | SIDER | ClinTox | MUV | HIV | BACE | Avg. | |
|---|---|---|---|---|---|---|---|---|---|
| AttrMask (Hu et al., 2020) | 70.2 ± 0.5 | 74.2 ± 0.8 | 62.5 ± 0.4 | 60.4 ± 0.6 | 68.6 ± 9.6 | 73.9 ± 1.3 | 74.3 ± 1.3 | 77.2 ± 1.4 | 70.2 |
| InfoGraph (Sun et al., 2020) | 69.2 ± 0.8 | 73.0 ± 0.7 | 62.0 ± 0.3 | 59.2 ± 0.2 | 75.1 ± 5.0 | 74.0 ± 1.5 | 74.5 ± 1.8 | 73.9 ± 2.5 | 70.1 |
| ContextPred (Hu et al., 2020) | 71.2 ± 0.9 | 73.3 ± 0.5 | 62.8 ± 0.3 | 59.3 ± 1.4 | 73.7 ± 4.0 | 72.5 ± 2.2 | 75.8 ± 1.1 | 78.6 ± 1.4 | 70.9 |
| GraphCL (You et al., 2021) | 67.5 ± 2.5 | 75.0 ± 0.5 | 62.8 ± 0.2 | 60.1 ± 1.3 | 78.9 ± 4.2 | 77.1 ± 1.0 | 75.0 ± 0.4 | 68.7 ± 7.8 | 70.6 |
| GraphMVP (Liu et al., 2022a) | 68.5 ± 0.2 | 74.5 ± 0.0 | 62.7 ± 0.1 | 62.3 ± 1.6 | 79.0 ± 2.5 | 75.0 ± 1.4 | 74.8 ± 1.4 | 76.8 ± 1.1 | 71.7 |
| GraphMAE (Hou et al., 2022b) | 70.9 ± 0.9 | 75.0 ± 0.4 | 64.1 ± 0.1 | 59.9 ± 0.5 | 81.5 ± 2.8 | 76.9 ± 2.6 | 76.7 ± 0.9 | 81.4 ± 1.4 | 73.3 |
| G2PTsmall (No pre-training) | 60.7 ± 0.3 | 66.4 ± 0.5 | 57.0 ± 0.3 | 61.6 ± 0.2 | 67.8 ± 1.1 | 45.8 ± 8.5 | 70.1 ± 7.5 | 68.8 ± 1.3 | 62.3 |
| G2PTbase (No pre-training) | 56.5 ± 0.2 | 67.4 ± 0.4 | 57.9 ± 0.1 | 60.2 ± 2.8 | 71.0 ± 5.6 | 60.1 ± 1.3 | 72.7 ± 1.1 | 73.4 ± 0.3 | 64.9 |
| G2PTsmall | 68.5 ± 0.5 | 74.7 ± 0.2 | 61.2 ± 0.1 | 61.7 ± 1.0 | 82.3 ± 2.2 | 74.9 ± 0.1 | 75.7 ± 0.4 | 81.3 ± 0.5 | 72.5 |
| G2PTbase | 71.0 ± 0.4 | 75.0 ± 0.3 | 63.0 ± 0.5 | 61.9 ± 0.2 | 82.1 ± 1.1 | 74.5 ± 0.3 | 76.3 ± 0.4 | 82.3 ± 1.6 | 73.3 |
🔼 표 9는 그래프 생성 성능에 대한 가장자리 순서의 민감도 분석 결과를 보여줍니다. 다양한 가장자리 순서(차수 기반, DFS, BFS, 균일)를 사용하여 G2PT 모델의 성능을 평가하고 유효성, 고유성, 참신성, 필터, FCD, SNN, Scaf 지표를 비교 분석했습니다. 각 가장자리 순서 방법에 따른 모델 성능의 차이를 통해 최적의 가장자리 순서 전략 선택의 중요성을 보여줍니다.
read the caption
Table 9: Sensitivity analysis on edge orderings.
Full paper#



















